9.E: Exercises on Electrochemistry

Exercise 9.E.1

Identify each half-reaction below as either oxidation or reduction.

a. [latex]\mathrm{Fe}^{3+}(aq) +3 \mathrm{e}^{-} \longrightarrow \mathrm{Fe}(s)[/latex]
b. [latex]\mathrm{Cr} (s) \longrightarrow \mathrm{Cr}^{3+}(aq)+3 \mathrm{e}^{-}[/latex]
c. [latex]\mathrm{MnO}_4^{2-}(aq) \longrightarrow \mathrm{MnO}_4^{-}(aq)+\mathrm{e}^{-}[/latex]
d.[latex]\mathrm{Li}^{+}(aq)+\mathrm{e}^{-} \longrightarrow \mathrm{Li}(s)[/latex]

Answer

a. reduction; b. oxidation; c. oxidation; d. reduction

Exercise 9.E.2

Assuming each pair of half-reactions below takes place in an acidic solution, write a balanced equation for the overall reaction.

a. [latex]\mathrm{Ca} \longrightarrow \mathrm{Ca}^{2+}+2 \mathrm{e}^{-}, \mathrm{F}_2+2 \mathrm{e}^{-} \longrightarrow 2 \mathrm{~F}^{-}[/latex]

b. [latex]\mathrm{Li} \longrightarrow \mathrm{Li}^{+}+\mathrm{e}^{-}, \mathrm{Cl}_2+2 \mathrm{e}^{-} \longrightarrow 2 \mathrm{Cl}^{-}[/latex]

c. [latex]\mathrm{Fe} \longrightarrow \mathrm{Fe}^{3+}+3 \mathrm{e}^{-}, \mathrm{Br}_2+2 \mathrm{e}^{-} \longrightarrow 2 \mathrm{Br}^{-}[/latex]

d. [latex]\mathrm{Ag} \longrightarrow \mathrm{Ag}^{+}+\mathrm{e}^{-}, \mathrm{MnO}_4^{-}+4 \mathrm{H}^{+}+3 \mathrm{e}^{-} \longrightarrow \mathrm{MnO}_2+2 \mathrm{H}_2 \mathrm{O}[/latex]

Answer

[latex](a) \mathrm{F}_2+\mathrm{Ca} \longrightarrow 2 \mathrm{~F}^{-}+\mathrm{Ca}^{2+} ; (b) $\mathrm{Cl}_2+2 \mathrm{Li} \longrightarrow 2 \mathrm{Li}^{+}+2 \mathrm{Cl}^{-} ;(c)

3 \mathrm{r}_2+2 \mathrm{Fe} \longrightarrow 2 \mathrm{Fe}^{3+}+6 \mathrm{Br}^{-} ; \text {(d) } \mathrm{MnO}_4^{-}+4 \mathrm{H}^{+}+3 \mathrm{Ag} \longrightarrow 3 \mathrm{Ag}^{+}+\mathrm{MnO}_2+2 \mathrm{H}_2 \mathrm{O}
[/latex]

Exercise 9.E.3

Write cell shorthand notations for the following cell reactions, using platinum as an inert electrode as needed.

a. Mg(s)+Ni²⁺(aq)⟶Mg²⁺(aq)+Ni(s)

b. 2Ag⁺(aq)+Cu(s)⟶Cu²⁺(aq)+2Ag(s)

c. Mn(s)+Sn(NO₃)₂(aq)⟶Mn(NO₃)₂(aq)+Sn(s)

d. 3CuNO₃(aq)+Au(NO₃)₃(aq)⟶3Cu(NO₃)₂(aq)+Au(s)

Answer

a. Mg(s)│Mg²⁺(aq)║Ni²⁺(aq)│Ni(s)

b. Cu(s)│Cu²⁺(aq)║Ag+(aq)│Ag(s)

c. Mn(s)│Mn²⁺(aq)║Sn²⁺(aq)│Sn(s)

d. Pt(s)│Cu⁺(aq), Cu²⁺(aq)║Au³⁺(aq)│Au(s)

Exercise 9.E.4

Why is a salt bridge necessary in galvanic cells?

Answer

Without the salt bridge, the circuit would be open (or broken) and no current could flow. With a salt bridge, each half-cell remains electrically neutral and current can flow through the circuit.

Exercise 9.E.5

An active (metal) electrode was found to lose mass as the oxidation-reduction reaction was allowed to proceed. Was the electrode an anode or a cathode? Explain.

Answer

Active electrodes participate in the oxidation-reduction reaction. Since metals form cations, the electrode would lose mass if metal atoms in the electrode were to oxidize and go into solution. Oxidation occurs at the anode.

Exercise 9.E.6

Identify where each reaction will take place (on the cathode or anode), balance the equation if necessary, and calculate the [latex]\mathrm{E^\circ_{cell}}[/latex].

1. [latex]\mathrm{Fe^{3+} (aq) + Ag(s) \rightarrow Fe^{2+}(aq) + Ag^+(aq)}[/latex]
2. [latex]\mathrm{Cu^{2+}(aq) + Zn(s) \rightarrow Cu(s) + Zn^{2+}(aq)}[/latex]
3. [latex]\mathrm{Cd(s) + Cu^{2+}(aq) \rightarrow Cd^{2+} + Cu(s)}[/latex]
4. [latex]\mathrm{Fe^{2+}(aq) + Cl_2(g) \rightarrow Fe^{3+}(aq) + 2Cl^-(aq)}[/latex]

Answer

Reduction: [latex]\mathrm{Fe^{3+} (aq) + e^- \rightarrow Fe^{2+}(aq)}[/latex] at the cathode (reduction occurs at the cathode)

Oxidation: [latex]\mathrm{Ag(s) \rightarrow Ag^+(aq) + e^-}[/latex] at the anode

The equation is already balanced.

[latex]\mathrm{E^{\circ}_{cell} = (0.771 - 0.800) = -0.029\;V}[/latex]

Reduction: [latex]\mathrm{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s)}[/latex] at the cathode, where reduction occurs

Reduction: [latex]\mathrm{Cl_2(g) + 2e^- \rightarrow 2Cl^-(aq)}[/latex] at the cathode

Oxidation: [latex]\mathrm{2(Fe^{2+}(aq) \rightarrow 2Fe^{3+}(aq) +e^-)}[/latex] at the anode

[latex]\mathrm{E^{\circ}_{cell} = 1.358 - (-0.440) = 1.798\;V}[/latex]

Oxidation: [latex]\mathrm{Cd(s) \rightarrow Cd^{2+} + 2e^-}[/latex] at the anode

Reaction is already balanced

[latex]\mathrm{E^{\circ}_{cell}= E^{\circ}_{(right)} - E^{\circ}_{(left)} = 0.340 - 0.743 = -0.403}[/latex]

Balance the equation, multiplying the iron half equation by 2 to equal the electrons

Oxidation: [latex]\mathrm{Zn(s) \rightarrow Zn^{2+}(aq) + 2e^-}[/latex] at the anode

Reaction is already balanced

[latex]\mathrm{E^{\circ}_{cell} = 0.340 - (-0.763) = 1.103\;V}[/latex]

Reduction: [latex]\mathrm{Cu^{2+}(aq) +2e^- \rightarrow Cu(s)}[/latex] at the cathode, where reduction occurs

Exercise 9.E.7

Calculate the theoretical cell voltage for the reaction between copper and zinc given that the overall reaction is:
[latex]\mathrm{Zn(s) + Cu^{2+}(aq) \rightarrow Zn^{2+}(aq) + Cu(s)}[/latex]

Answer

Oxidation: [latex]\mathrm{Cu(s) \rightarrow Cu^{2+}(aq) + 2e^- \hspace{1 pt}\quad E^\circ= 0.340\: V}[/latex]
Reduction: [latex]\mathrm{Zn^{2+}(aq) + 2e^- \rightarrow Zn(s) \quad E^\circ= -0.763\: V}[/latex]
[latex]\mathrm{E^\circ_{cell}= -0.763\:V - 0.340\:V = -1.103\:V}[/latex]

Exercise 9.E.8

Use data from the standard electrode reduction potentials table to predict whether the reactions below are spontaneous in the forward reaction (All reactants and products are in their standard states):

1. [latex]\mathrm{Cu (s) + 2Ag^+ (aq) \rightarrow Cu^{2+} (aq) + 2Ag (s)}[/latex]
2. [latex]\mathrm{2Al (s) + 3Zn^{2+} (aq) \rightarrow 2Al^{3+} (aq) + 3Zn (s)}[/latex]
3. [latex]\mathrm{Fe^{2+} (aq) + Ag^+ (aq) \rightarrow Fe^{3+} (aq) + Ag (s)}[/latex]
4. [latex]\mathrm{2Fe^{2+} (aq) + I_2 (s) \rightarrow 2Fe^{3+} (aq) + 2I^- (aq)}[/latex]

Answer

Cell reaction: [latex]\mathrm{Cu(s) + 2Ag^+ (aq) \rightarrow 2Cu^{2+} (aq) + 2Ag (s)}[/latex]

Oxidation: [latex]\mathrm{ Cu (s) \rightarrow Cu^{2+} + 2e^-}[/latex]
Reduction: [latex]\mathrm{(Ag^+ (aq) + e^- \rightarrow ​​ Ag (s)​​​​​)\times2}[/latex]

[latex]\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E^\circ_{(reduction)}-E^\circ_{(oxidation)}} \\
& =\mathrm{E^\circ_{Ag^+/Ag} - E^\circ_{Cu/Cu^{2+} }} \\
& =\mathrm{0.7991-0.3394= +0.4597\:V}
\end{align}[/latex]
The cell potential is positive, therefore the spontaneous reaction will occur in the forward reaction.

Cell reaction: [latex]\mathrm{2Al (s) + 3Zn^{2+} (aq) \rightarrow 2Al^{3+} (aq) + 3Zn (s)}[/latex]

Oxidation: [latex]\mathrm{(Fe^{3+}(aq) + e^- \rightarrow Fe^{2+}(aq)​)\times2}[/latex]
Reduction: [latex]\mathrm{I_2(s) + 2e^- \rightarrow 2I^-(aq)}[/latex]
[latex]\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E^\circ_{(reduction)}-E^\circ_{(oxidation)}} \\
& =\mathrm{E^\circ_{I_2/2I^-} - E^\circ_{Fe^{2+}/Fe^{3+}}} \\
& =\mathrm{0.535-0.769= -0.234\:V}
\end{align}[/latex]
The cell potential is negative, therefore the spontaneous reaction will not occur in the forward reaction.

Oxidation: [latex]\mathrm{Fe^{2+} (aq) \rightarrow Fe^{3+} (aq) + e^- }[/latex]
Reduction: [latex]\mathrm{Ag(s)\rightarrow Ag^+(aq) + e^-}[/latex]
[latex]\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E^\circ_{(reduction)}-E^\circ_{(oxidation)}} \\
& =\mathrm{E^\circ_{Ag^+/Ag} - E^\circ_{Fe^{2+}/Fe^{3+}}} \\
& =\mathrm{0.7991-0.769= +0.0301\:V}
\end{align}[/latex]
The cell potential is positive, therefore the spontaneous reaction will occur in the forward reaction.

Cell reaction: [latex]\mathrm{2Fe^{2+}(aq) + I_2(s) \rightarrow 2Fe^{3+}(aq) + 2I^- (aq)}[/latex]

Oxidation: [latex]\mathrm{(Al (s) \rightarrow Al^{3+} + 3e^- )\times2}[/latex]
Reduction: [latex]\mathrm{(Zn^{2+}(aq) +2e^-\rightarrow Zn(s) )\times3}[/latex]
[latex]\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E^\circ_{(reduction)}-E^\circ_{(oxidation)}} \\
& =\mathrm{E^\circ_{Zn^{2+}/Zn} - E^\circ_{Al/Al^{3+}}} \\
& =\mathrm{-0.7621-(-1.676)= +0.9139\:V}
\end{align}[/latex]
The cell potential is positive, therefore the spontaneous reaction will occur in the forward reaction.

Cell reaction: [latex]\mathrm{Fe^{2+}(aq) + Ag^+ (aq) \rightarrow Fe^{3+} (aq) + Ag (s)}[/latex]

Exercise 9.E.9

Write cell reactions for the electrochemical cells diagrammed, and use data from the table of standard electrode potentials to calculate [latex]\mathrm{E^\circ_{cell}}[/latex] for each reaction.

1. [latex]\mathrm{Fe (s)|Fe^{2+} (aq)||Zn (s) |Zn^{2+} (aq)}[/latex]
2. [latex]\mathrm{Na(s)|Na^+(aq)||Cl_2(g)|Cl^-(aq)}[/latex]
3. [latex]\mathrm{Co(s)|Co^{2+} (aq)||Mn^{2+} (aq)|Mn(s)}[/latex]
4. [latex]\mathrm{Pt(s)|Fe^{2+} (aq), Fe^{3+} (aq)||Pb^{2+}(aq)|Pb(s)}[/latex]

Answer

Oxidation: [latex]\mathrm{Fe(s) \rightarrow Fe^{2+} (aq) + 2e^- \hspace{74 pt} \quad E^\circ = -(-0.440\:V)}[/latex]

Reduction: [latex]\mathrm{Zn^{2+} (aq) + 2e^- \rightarrow Zn(s) \hspace{68 pt} \quad E^\circ = -0.7621\:V}[/latex]
Net Reaction: [latex]\mathrm{Fe(s) + Zn^{2+} (aq) \rightarrow Fe^{2+} (aq) + Zn(s) \quad E^\circ_{cell}= -0.3321\: V}[/latex]

Oxidation: [latex]\mathrm{Na(s) \rightarrow Na^+ (aq) + e^- \hspace{83 pt}\quad E^\circ = -(-2.7144\:V)}[/latex]

Reduction: [latex]\mathrm{Pb^{2+} (aq) + 2e^- \rightarrow Pb(s) \hspace{76 pt}\quad E^\circ= -0.125\:V}[/latex]
Net Reaction: [latex]\mathrm{2Fe^{2+} + Pb^{2+}(aq) \rightarrow 2Fe^{3+} (aq) + Pb(s) \quad E^\circ_{cell} = -0.896\:V}[/latex]

Reduction: [latex]\mathrm{Mn^{2+} (aq) + 2e^- \rightarrow Mn(s) \hspace{71 pt}\quad E^\circ = -1.182\:V}[/latex]
Net Reaction: [latex]\mathrm{Co(s) + Mn^{2+} (aq) \rightarrow Co^{2+} (aq) + Mn(s) \quad E^\circ_{cell}= -0.905\:V}[/latex]

Oxidation: [latex]\mathrm{(Fe^{2+} (aq) \rightarrow Fe^{3+} (aq) + e^-)\times2 \hspace{47 pt}\quad E^\circ= -(-0.771\:V)}[/latex]

Reduction: [latex]\mathrm{Cl_2 (g) + e^- \rightarrow 2Cl^-(aq) \hspace{73 pt}\quad E^\circ = 1.3601\:V}[/latex]
Net Reaction: [latex]\mathrm{Na(s) + Cl_2(g) \rightarrow Na^+ (aq) + 2Cl^-(aq) \quad E^\circ_{cell}= -0.905\:V}[/latex]

Oxidation: [latex]\mathrm{Co(s) \rightarrow Co^{2+} (aq) + 2e^- \hspace{80 pt}\quad E^\circ= -(-0.277\:V)}[/latex]

Exercise 9.E.10

For each of the following reactions below, draw a voltaic cell. In your drawing include the anode, cathode, and show the flow of electrons. Balance the equation and calculate the [latex]\mathrm{E^\circ_{cell}}[/latex].

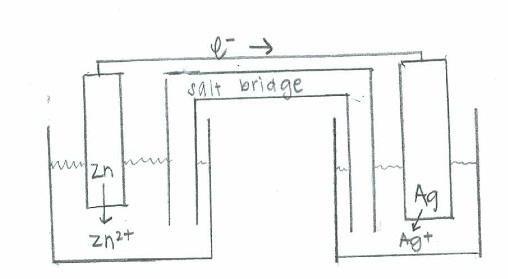
1. [latex]\mathrm{Zn (s) + Ag^+ (aq) \rightarrow Ag(s) + Zn^{2+}(aq)}[/latex]
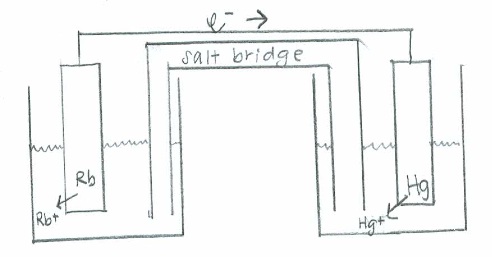
2. [latex]\mathrm{Rb(s) + Hg^{2+}(aq) \rightarrow Rb^+(aq) + Hg (s)}[/latex]
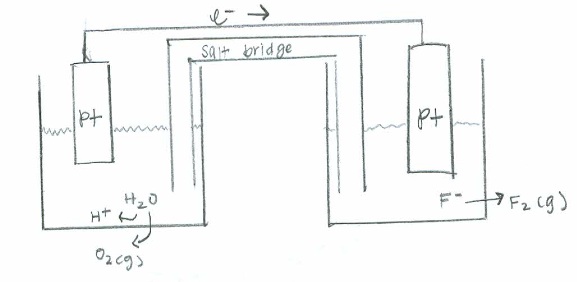
3. [latex]\mathrm{F_2(g) + H_2O(l) \rightarrow 4F^-(aq) + O_2 (g) + H^+ (aq)}[/latex]
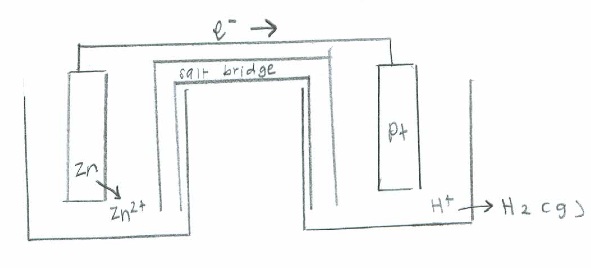
4. [latex]\mathrm{Zn (s) + H^+ (aq) \rightarrow Zn^{2+} (aq) + H_2 (g)}[/latex]

Answer

Oxidation: [latex]\mathrm{Zn(s) \rightarrow Zn^{2+} (aq) + 2e^- \hspace{38.5 pt}\quad {-E}^\circ=0.763\:V}[/latex]

Reduction: [latex]\mathrm{(e^- + Ag^+(aq) \rightarrow Ag (s))\times2 \hspace{24 pt}\quad E^\circ=0.337\:V}[/latex]

Net: [latex]\mathrm{Zn (s) + 2Ag^+ (aq) \rightarrow 2Ag(s) + Zn^{2+}(aq) \quad E^\circ_{cell}=1.100\:V}[/latex]

Oxidation: [latex]\mathrm{(Rb(s) \rightarrow Rb^+(aq) + e^-)\times 2 \hspace{22 pt}\quad {-E}^\circ=+2.93\:V}[/latex]

Reduction: [latex]\mathrm{Hg^{2+}(aq) + 2e^- \rightarrow Hg (s) \hspace{43 pt}\quad E^\circ=0.86\:V}[/latex]

Net: [latex]\mathrm{2Rb(s) + Hg^{2+}(aq)\rightarrow 2Rb^+(aq) + Hg (s) \quad E^\circ_{cell}=3.79\:V}[/latex]

Oxidation: [latex]\mathrm{2H_2O (l) \rightarrow O_2(g) + 4H^+(aq) + 4e^- \hspace{31 pt} \quad {-E}^\circ=-1.229\:V}[/latex]

Reduction: [latex]\mathrm{(2e^-+F_2(g) \rightarrow 2F^-(aq))\times2 \hspace{60 pt} \quad E^\circ=2.866\:V}[/latex]

Net: [latex]\mathrm{2F_2(g) + 2H_2O(l) \rightarrow 4F^-(aq) + O_2 (g) + 4H^+ (aq) \quad E^\circ_{cell}=1.637\:V}[/latex]

Oxidation: [latex]\mathrm{2H_2O (l) \rightarrow O_2(g) + 4H^+(aq) + 4e^- \hspace{31 pt} \quad {-E}^\circ=-1.229\:V}[/latex]

Reduction: [latex]\mathrm{(2e^-+F_2(g) \rightarrow 2F^-(aq))\times2 \hspace{60 pt} \quad E^\circ=2.866\:V}[/latex]

Net: [latex]\mathrm{2F_2(g) + 2H_2O(l) \rightarrow 4F^-(aq) + O_2 (g) + 4H^+ (aq) \quad E^\circ_{cell}=1.637\:V}[/latex]

Exercise 9.E.11

What are the [latex]\mathrm{\Delta G^\circ}[/latex] for the reactions below?

1. [latex]\mathrm{Ti (s) + Cr^{2+}(aq) \rightarrow Ti^{2+}(aq) + Cr (s)}[/latex]
2. [latex]\mathrm{2Cu^+(aq) + Sn^{4+} (aq) \rightarrow 2Cu^{2+}(aq) + Sn^{2+}(aq)}[/latex]
3. [latex]\mathrm{2Cl_2(g) + 2H_2O(l) \rightarrow O_2(g) + 4H^+(aq) + 4Cl^-(aq)}[/latex]

Answer

Oxidation: [latex]\mathrm{Ti(s)\rightarrow Ti^{2+}(aq) + 2e^- \hspace{29.5 pt}\quad {-E}^\circ=+1.63\:V}[/latex]

Reduction: [latex]\mathrm{Cr^{2+}(aq) + 2e^- \rightarrow Cr (s) \hspace{30.5 pt}\quad E^\circ=-0.90\:V}[/latex]

Net: [latex]\mathrm{Ti (s) + Cr^{2+}(aq) \rightarrow Ti^{2+}(aq) + Cr (s) \quad E^\circ_{cell}=0.73\:V}[/latex]

[latex]\mathrm{\Delta G^\circ=-nF E^\circ_{cell}=-(2\: mole\: e^-)(96,485\: C/mol\: e^-)(0.73\:V)=-140,868.1\:J=-1.41\times10^2\:KJ}[/latex]

Oxidation: [latex]\mathrm{Sn^{2+}(aq) \rightarrow 2e^- + Sn^{4+}(aq) \hspace{55 pt}\quad {-E}^\circ=-0.154\:V}[/latex]

Reduction: [latex]\mathrm{(Cl_2(g) + 2e^- \rightarrow 2 Cl^-(aq)) \times2 \hspace{60 pt}\quad E^\circ=1.358}[/latex]

Net: [latex]\mathrm{2Cl_2(g) + 2H_2O(l) \rightarrow O_2(g) + 4H^+(aq) + 4Cl^-(aq) \quad E^\circ_{cell}=0.129\:V}[/latex]

[latex]\mathrm{\Delta G^\circ=-nFE^\circ_{cell}=-(4\: mole\: e^-)(96,485\: C/mol\: e^-)(0.129\:V)= -49,786.26\: J= -4.98\times10^4\: KJ}[/latex]

Reduction: [latex]\mathrm{(Cu^{2+}(aq) + e^- \rightarrow Cu^+(aq))\times2 \hspace{39 pt}\quad E^\circ=0.159\:V}[/latex]

Net: [latex]\mathrm{2Cu^+(aq) + Sn^{4+} (aq) \rightarrow 2Cu^{2+}(aq) + Sn^{2+}(aq) \quad E^\circ_{cell}=0.005\:V}[/latex]

[latex]\mathrm{\Delta G^\circ=-nFE^\circ_{cell}=-(2\: mole\: e^-)(96,485\: C/mol\: e^-)(0.005\:V)=-946.85\:J=-0.965\:KJ}[/latex]

Oxidation: [latex]\mathrm{2H_2O(l) \rightarrow O_2(g) + 4H^+(aq) + 4e^- \hspace{39 pt}\quad {-E}^\circ=-1.229\:V}[/latex]

Exercise 9.E.12

Find [latex]\mathrm{E^\circ}[/latex], [latex]\mathrm{\Delta G^\circ}[/latex], [latex]\ce{K}[/latex], and given that the reactants and products are in their standard state, if they go to completion or not for the following reaction:

[latex]\mathrm{2BrO_3^-(aq) + 12H^+(aq) + 10SO_4^{2-}(aq) \rightarrow 5S_2O_8^{2-}(aq) + Br_2(l) + 6H_2O (l)}[/latex]

Answer

Oxidation: [latex]\mathrm{(2SO_4^{2-}(aq) \rightarrow S_2O_8^{2-}(aq) + 2e^-)\times5 \hspace{127 pt}\quad {-E}^\circ=-2.01\:V}[/latex]

Reduction: [latex]\mathrm{2BrO_3^-(aq) + 12H^+(aq) +10e^- \rightarrow Br_2(l) + 6H_2O (l) \hspace{67 pt}\quad E^\circ=1.478\:V}[/latex]

Net: [latex]\mathrm{2BrO_3^-(aq) + 12H^+(aq) + 10SO_4^{2-}(aq) \rightarrow5S_2O_8^{2-}(aq) + Br_2(l) + 6H_2O (l) \quad E^\circ_{cell}=-0.532\:V}[/latex]

[latex]\mathrm{\Delta G^\circ=-nFE^\circ_{cell}=-(10\: mole\: e^-)(96,485\: C/mol\: e^-)(-0.532\:V)=5.13\times10^2\:KJ/mol}[/latex]

[latex]\mathrm{\Delta G^\circ=-RT\ln K}[/latex]

[latex]\mathrm{5.13\times10^2\:KJ/mol = -(-8.314\:KJ/mol)(298.15\:K)\ln K}[/latex]

[latex]\mathrm{K=8.13\times10^{-1}}[/latex]

Since [latex]\ce{K}[/latex] is small ([latex]\mathrm{<1}[/latex]) the reaction will not go to completion.

Exercise 9.E.13

A voltaic cell has an [latex]\mathrm{E_{cell}}[/latex] value of 1.536 V. What is the concentration of [latex]\ce{Ag+}[/latex] in the cell?

[latex]\mathrm{Zn(s) | Zn^{2+}(2.00\:M) || Ag^+(x\:M) | Ag(s)}[/latex]

Answer

First, determine [latex]\mathrm{E^\circ_{cell}}[/latex]:
Oxidation: [latex]\mathrm{Zn(s) \rightarrow Zn^{2+}(aq) + 2e^- \hspace{77 pt}\quad E^\circ= -0.763\: V}[/latex]
Reduction: [latex]\mathrm{2Ag^+(aq) + 2e^- \rightarrow Ag(s) \hspace{70 pt}\quad E^\circ= 0.800\: V}[/latex]
Net Reaction: [latex]\mathrm{Zn(s) + 2Ag^+(aq) \rightarrow Zn^{2+}(aq) + Ag(s) \quad E^\circ_{cell}= 1.563\: V}[/latex]

Second, use Nernst equation to calculate [latex]\ce{[Ag+]}[/latex]
[latex]\mathrm{E=E^\circ_{cell}-\dfrac{0.0592}{n}\log\dfrac{[Zn^{2+}]}{[Ag^+]^2}}[/latex]
[latex]\mathrm{1.536=1.563-\dfrac{0.0592}{2}\log\dfrac{2}{x^2}}[/latex]
[latex]\mathrm{-0.027\left (\dfrac{-2}{0.0592} \right )=log\dfrac{2}{x^2}}[/latex]
[latex]\mathrm{8.168=\dfrac{2}{x^2}}[/latex]
[latex]\mathrm{x^2=0.2448}[/latex]
[latex]\mathrm{x=0.495=[Ag^+]}[/latex]

Exercise 9.E.14

Using the Nernst equation, find [latex]\mathrm{E_{cell}}[/latex] for the following cells:

1. [latex]\mathrm{Al(s) | Al^{3+}(0.30\:M) || Fe^{2+}(1.1\:M) | Fe(s)}[/latex]
2. [latex]\mathrm{Co(s) | Co^{2+}(0.6\:M) || Fe^{3+}(1.0\:M), Fe^{2+}(0.9\:M) | Pt(s)}[/latex]

Answer

First, determine [latex]\mathrm{E^\circ_{cell}}[/latex]

Oxidation: [latex]\mathrm{2Al(s) \rightarrow 2Al^{3+}(aq) + 6e^- \hspace{115 pt} \quad E^\circ_{cell}= 1.676\: V}[/latex]
Reduction: [latex]\mathrm{3Fe^{3+}(aq) + 6e^- \rightarrow 3Fe(s) \hspace{110 pt} \quad E^\circ_{cell}= -0.440\: V}[/latex]
Net Reaction: [latex]\mathrm{2Al(s) + 3Fe^{2+}(1.1\:M) \rightarrow 2Al^{3+}(0.30\:M) + 3Fe(s) \quad E^\circ_{cell}= 1.236\: V}[/latex]

Second, use Nernst equation to calculate [latex]\mathrm{E_{cell}}[/latex]
[latex]\mathrm{E_{cell}=E^\circ_{cell}-\dfrac{0.0592}{n}\log\dfrac{[Al^{3+}]^2}{[Fe^{2+}]^3}}[/latex]
[latex]\mathrm{E_{cell}=1.236-\dfrac{0.0592}{6}\log\dfrac{(0.3)^2}{(1.1)^3}}[/latex]
[latex]\mathrm{E_{cell}=1.247}[/latex]

First, determine [latex]\mathrm{E^\circ_{cell}}[/latex]

Oxidation: [latex]\mathrm{Co(s) \rightarrow Co^{2+}(aq) + 2e^- \hspace{131 pt}\quad {-E}^\circ_{cell}=0.277\: V}[/latex]
Reduction: [latex]\mathrm{2Fe^{3+}(aq) + 2e^- \rightarrow 2Fe^{2+}(aq) \hspace{112 pt}\quad E^\circ_{cell}=0.771}[/latex]
Net Reaction: [latex]\mathrm{Co(s) + 2Fe^{3+}(1.0\:M) \rightarrow Co^{2+}(0.6\:M) +2Fe^{2+}(0.9\:M) \quad E^\circ_{cell}=1.048\: V}[/latex]

Second, use Nernst equation to calculate [latex]\mathrm{E_{cell}}[/latex]
[latex]\mathrm{E_{cell}=E^\circ_{cell}-\dfrac{0.0592}{n}\log\dfrac{[Fe^{2+}]^2[Co^{2+}]}{[Fe^{3+}]^2}}[/latex]
[latex]\mathrm{E_{cell}=1.048-\dfrac{0.0592}{2}\log\dfrac{(0.9)^2(0.6)}{(1.0)^2}}[/latex]
[latex]\mathrm{E_{cell}=1.057\: V}[/latex]

Exercise 9.E.15

If [latex]\ce{[Cu^2+]}[/latex] is maintained at 1.0 M, what is the minimum [latex]\ce{[Ag+]}[/latex] for which the reaction given below, is spontaneous in the forward direction?

[latex]\mathrm{Cu(s) + 2Ag^+(aq) \rightarrow Cu^{2+}(aq) + 2Ag(s)}[/latex]

Answer

Remember – in order for the reaction to be spontaneous, [latex]\mathrm{\Delta G<0}[/latex].

Important equations:

[latex]\mathrm{E^\circ_{cell} = E^\circ_{cathode} - E^\circ_{anode}}[/latex]
[latex]\mathrm{0 = E^\circ - \dfrac{RT}{nF}\ln Q \:\Rightarrow \: E^\circ= \dfrac{RT}{nF}\ln Q}[/latex]
[latex]\mathrm{Q = [Cu^{2+}/ Ag^+]}[/latex]

Write the equation as a cell diagram:

[latex]\mathrm{Cu(s) | Cu^{2+}(aq) || Ag^+(aq) | Ag(s)}[/latex]
Oxidation: [latex]\mathrm{Cu(s) \rightarrow Cu^{2+}(aq) + 2e^- \hspace{19 pt}\quad E^\circ= -0.340}[/latex]
Reduction: [latex]\mathrm{(Ag^+(aq) + e^- \rightarrow Ag(s))\times2 \quad E^\circ= 0.800}[/latex]
Net reaction: [latex]\mathrm{Cu(s) + 2Ag^+(aq) \rightarrow Cu^{2+}(aq) + 2Ag(s)}[/latex]
[latex]\mathrm{E^\circ_{cell} = 0.800 - 0.340 = 0.46\:V}[/latex]
[latex]\mathrm{0.46 = \dfrac{RT}{2F}\ln\dfrac{[1]}{[Ag^+]}}[/latex]
[latex]\mathrm{0.46 = \dfrac{RT}{2F}(\ln1-\ln[Ag^+])}[/latex]
[latex]\mathrm{0.46 = -\dfrac{RT}{2F}\ln[Ag^+]}[/latex]
[latex]\mathrm{0.46 = -\dfrac{(8.3145)(298)}{2(96485)}\ln[Ag^+]}[/latex]
Solve for [latex]\ce{[Ag^+]}[/latex]
[latex]\mathrm{[Ag^+] = 2.76\times10^{-16}\: M}[/latex]

Exercise 9.E.16

Determine the anode and cathode of the following reactions. Then, calculate the reaction’s equilibrium constant, K.

1. [latex]\ce{Ca^2+(aq) + 2Li(s) \rightarrow Ca(s) + 2Li+(aq)}[/latex]
2. [latex]\ce{H2SO3(aq) + 4H+(aq) + 4[Fe(CN)6]^4- (aq) \rightarrow S(s) + 3H2O(l) + 4[Fe(CN)6]^3-}[/latex]

Answer

[latex]\textrm{Cathode: } \mathrm{Ca^{2+}(aq) + 2e^- \rightarrow Ca(s)} \quad \mathrm{E^{\circ}=-2.84\:V}[/latex]
[latex]\textrm{Anode: } \mathrm{2Li(s)\rightarrow 2Li^+(aq)+2e^-} \quad \hspace{11 pt} \mathrm{E^{\circ}=-3.040\:V}[/latex]

[latex]\begin{align}
\mathrm{E^{\circ}_{cell}} & = \mathrm{E^{\circ}_{cathode}- E^{\circ}_{anode}} \\
& = \mathrm{-2.84 - (3.040)} \\
& = \mathrm{0.2\:V}
\end{align}[/latex]

[latex]\mathrm{E^\circ_{cell}=\dfrac{0.026\,V}{n}\ln K}[/latex]​

[latex]\mathrm{0.2\,V=\dfrac{0.026\,V}{2}\ln K}[/latex]​

[latex]\mathrm{\ln K=15.38}[/latex]​

[latex]\mathrm{K=4.8\times10^6}[/latex]​

[latex]\textrm{Cathode: } \ce{H2SO3(aq) + 4H+(aq) + 4e- \rightarrow S(s) + 3H2O(l)} \quad \mathrm{E^{\circ}=+0.449\:V}[/latex]
[latex]\textrm{Anode: } \ce{4[Fe(CN)6]^4- (aq) \rightarrow 4[Fe(CN)6]^3- (aq) + 4e-} \quad \hspace{18 pt} \mathrm{E^{\circ}=+0.361\:V}[/latex]

[latex]\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E^{\circ}_{cathode}- E^{\circ}_{anode}} \\
& = \mathrm{0.449-0.361} \\
& = \mathrm{0.088\:V}
\end{align}[/latex]

[latex]\mathrm{E^\circ_{cell}=\dfrac{0.026\,V}{n}\ln K}[/latex]​

[latex]\mathrm{0.088\,V=\dfrac{0.026\,V}{4}\ln K}[/latex]​

[latex]\mathrm{\ln K=13.54}[/latex]​

[latex]\mathrm{K=7.6\times10^5}[/latex]​

Exercise 9.E.17

Solve for [latex]\mathrm{E_{cell}}[/latex] of the following voltaic cell

[latex]\mathrm{Cu(s) | Cu^{2+} (0.01\:M) || Cu^{2+} (0.1\:M) | Cu(s)}[/latex]

Answer

First solve for [latex]\mathrm{E^\circ_{cell}}[/latex]

Oxidation: [latex]\mathrm{Cu(s) \rightarrow Cu^{2+} + 2e^- \quad E^\circ = -0.340}[/latex]

Reduction: [latex]\mathrm{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s) \quad E^\circ= +0.340}[/latex]

[latex]\mathrm{E^\circ_{cell} = E^\circ_{cathode} - E^\circ_{anode}}[/latex]

[latex]\mathrm{0.340-(-0.340) = 0.68}[/latex]

Then use the Nernst Equation to solve for [latex]\mathrm{E_{cell}}[/latex]

[latex]\begin{align}
\mathrm{E_{cell}} & = \mathrm{E^\circ_{cell} - \dfrac{0.0257}{2}\ln Q} \\
& = \mathrm{0.68 - \dfrac{0.0257}{2}\ln\dfrac{0.01\:M}{0.1\:M}} \\
\mathrm{E_{cell}} & = \mathrm{0.7096\:V}
\end{align}[/latex]

Exercise 9.E.18

1. Determine if the cell reaction for the following cell will proceed spontaneously in the forward direction.

[latex]\mathrm{Pb(s) | Pb^{2+} (1.00\:M) || Cu^{2+} (1.00\:M) | Cu(s)}[/latex]

2. By using the Nernst equation, [latex]\mathrm{\dfrac{-0.0592}{2}\log\dfrac{[Pb^{2+}]}{[Cu^{2+}]}}[/latex] must be greater than what value in order to make the reaction non-spontaneous?

Answer

Determine [latex]\mathrm{E^\circ_{cell}}[/latex]

Oxidation: [latex]\mathrm{Pb(s) \rightarrow Pb^{2+}(aq) + 2e^- \hspace{113.5 pt}\quad E^\circ_{cell}= -0.125\: V}[/latex]
Reduction: [latex]\mathrm{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s) \hspace{109 pt}\quad E^\circ_{cell}= 0.340\: V}[/latex]
Net Reaction: [latex]\mathrm{Pb(s) + Cu^{2+}(1.00\:M) \rightarrow Pb^{2+}(1.00\:M) + Cu(s) \quad E^\circ_{cell}= 0.465\: V}[/latex]

[latex]\mathrm{E^\circ_{cell}}[/latex] is positive, therefore the cell reaction for the cell will proceed spontaneously in the forward direction.

[latex]\mathrm{\dfrac{-0.0592}{2}\log\dfrac{[Pb^{2+}]}{[Cu^{2+}]} > 0.465}[/latex]