7.E: Buffers, Titrations and Solubility Equilibria (Exercises)

Exercise 7.E.1

What is the role of a buffer in chemistry and biology?

Answer

The role of a buffer in chemistry and biology is to resist pH changes upon the addition of an acid or base.

Exercise 7.E.2

Explain why the most effective buffers are those that contain approximately equal amounts of the weak acid and its conjugate base.

Answer

The most effective buffers are those that contain approximately equal amounts of the weak acid and its conjugate base because when placed in the Henderson-Hasselbalch equation the [latex]pH[/latex] approximately equals the [latex]pK_{a}[/latex]. This is the goal because the more the ratio needs to differ to achieve the desired pH, the less effective the buffer and it should not differ by more than tenfold.

Exercise 7.E.3

If you were given a solution of sodium acetate, describe a way you could convert the solution to a buffer.

Answer

Sodium acetate is a salt, therefore it can’t be regarded as an acid or a base. One way to convert the solution to a buffer is to combine sodium acetate with a weak acid such as acetic acid. The sodium acetate would react with the hydronium ions and the acetic acid would react with hydroxide ions to prevent drastic changes in pH.

Exercise 7.E.4

Benzenesulfonic acid ([latex]pKa = 0.70[/latex]) is synthesized by treating benzene with concentrated sulfuric acid. Calculate the following:

1. the [latex]pH[/latex] of a 0.286 M solution of benzenesulfonic acid
2. the pH after adding enough sodium benzenesulfonate to give a final benzenesulfonate concentration of 0.100 M

Answer

a. [latex]pH=-log([H^{+}])=-log(0.2388)=0.62[/latex]

[latex]K_a=\frac{[H^{+}][A^{-}]}{[HA]} \rightarrow K_a=\frac{[H^{+}]^{2}}{[HA]} \rightarrow [H^{+}]= \sqrt{K_a\times[HA]}=\sqrt{10^{-0.70} \times 0.286\,M}=0.2388[/latex]

b. [latex]pH=-log([H^{+}])=-log(0.14125)=0.850[/latex]

[latex]K_a=\frac{[H^{+}][A^{-}]}{[HA]} \rightarrow K_a=\frac{[H^{+}]^{2}}{[HA]} \rightarrow [H^{+}]= \sqrt{K_a\times[HA]}=\sqrt{10^{-0.70} \times 0.100\,M}=0.14125[/latex]

Exercise 7.E.5

Which of the following will produce a buffer solution? Explain your reasoning in each case.

1. mixing 100 mL of 0.1 M [latex]HCl[/latex] and 100 mL of 0.1 M sodium fluoride
2. mixing 50 mL of 0.1 M [latex]HCl[/latex] and 100 mL of 0.1 M sodium fluoride
3. mixing 100 mL of 0.1 M hydrofluoric acid and 100 mL of 0.1 M [latex]HCl[/latex]
4. mixing 100 mL of 0.1 M hydrofluoric acid and 50 mL of 0.1 M [latex]NaOH[/latex]
5. mixing 100 mL of 0.1 M sodium fluoride and 50 mL of 0.1 M [latex]NaOH[/latex].

Answer

a. This will not produce a buffer solution because the hydrochloric acid completely neutralizes the sodium fluoride to give sodium chloride.

b. This will produce a buffer solution because the hydrochloric acid neutralizes only half of the acetic acid to give a solution containing equal amounts of hydrofluoric acid and sodium chloride.

c. This will not produce a buffer solution because hydrofluoric acid is a weak acid and hydrochloric acid is a strong acid.

d. This will produce a buffer solution because the solution will contain a 2:1 ratio of hydrofluoric acid and sodium hydroxide.

e. This will not produce a buffer solution solution because sodium fluoride is a weak base and sodium hydroxide is a strong base.

Exercise 7.E.6

What will be the pH of a buffer solution prepared from 0.20 mol NH₃, 0.40 mol NH₄NO₃, and just enough water to give 1.00 L of solution?

Answer

pH = 8.95

Exercise 7.E.7

A buffer solution is prepared from equal volumes of 0.200 M acetic acid and 0.600 M sodium acetate. Use 1.80 × 10⁻⁵ as K_a for acetic acid.

(a) What is the pH of the solution?

(b) Is the solution acidic or basic?

(c) What is the pH of a solution that results when 3.00 mL of 0.034 M HCl is added to 0.200 L of the original buffer?

Answer

(a) pH = 5.222; (b) The solution is acidic. (c) pH = 5.220

Exercise 7.E.8

Why are buffers usually used only within approximately one pH unit of the [latex]pK_a[/latex] or [latex]pK_b[/latex] of the parent weak acid or base?

Answer

Buffers are usually used only within approximately one [latex]pH[/latex] unit of the [latex]pK_a[/latex] or [latex]pK_b[/latex] of the parent weak acid or base because the ability of a buffer solution to maintain a nearly constant pH due to a small amount of acid or base is greatest at the [latex]pK_a[/latex] and decreases as the pH of the solution goes above or below the [latex]pK_a[/latex].

[latex]pH=pK_a+log(\frac{[B]}{[A]})[/latex]

When [latex]\frac{[B]}{[A]}=10[/latex]: [latex]pH=pK_a+1[/latex]

When [latex]\frac{[B]}{[A]}=\frac{1}{10}[/latex]: [latex]pH=pK_a-1[/latex]

Exercise 7.E.9

How much solid NaCH₃CO₂•3H₂O must be added to 0.300 L of a 0.50-M acetic acid solution to give a buffer with a pH of 5.00? (Hint: Assume a negligible change in volume as the solid is added.)

Answer

37 g (0.27 mol)

Exercise 7.E.10

The titration curve for a monoprotic acid can be divided into four regions: the starting point, the region around the midpoint of the titration, the equivalence point, and the region after the equivalence point. For which region would you use each approach to describe the behavior of the solution?

1. a buffer
2. a solution of a salt of a weak base
3. a solution of a weak acid
4. diluting a strong base

Answer

a. I would use the region around the midpoint of the titration to describe the behavior of a buffer because the midpoint of the titration is defined as the point at which exactly enough acid or base has been added to neutralize one-half of the acid or the base originally present while maintaining a relatively constant pH.

b. I would use the equivalence point region to describe the behavior of a solution of a salt of a weak base because at this point the amount of titrant added is enough to completely neutralize the solution.

c. I would use the starting point region of the titration curve to describe the behavior of the solution of a weak acid because it is expected to be at a higher pH than a strong acid but lower than [latex]pH[/latex] 7.

d. I would use the region after the equivalence point to describe the dilution of a strong base because in this region one can predict the pH by simply taking into account the amount of excess base.

Exercise 7.E.11

Why is the portion of the titration curve that lies below the equivalence point of a solution of a weak acid displaced upward relative to the titration curve of a strong acid? How are the slopes of the curves different at the equivalence point? Why?

Answer

The portion of the titration curve that lies below the equivalence point of a solution of a weak acid is displaced upward relative to the titration curve of a strong acid because the starting point of a weak acid is at a higher [latex]pH[/latex] compared to that of a strong acid. The slope for a strong acid is greater compared to that of a weak acid because when a weak acid is neutralized, the solution that remains is basic because the acid’s conjugate base remains in solution.

Exercise 7.E.12

Predict whether each solution will be neutral, basic, or acidic at the equivalence point of each titration.

1. An aqueous solution of [latex]NaOH[/latex] is titrated with 0.100 M [latex]HCl[/latex].
2. An aqueous solution of ethylamine ([latex]CH_3CH_2NH_2[/latex]) is titrated with 0.150 M [latex]HNO_{3}[/latex]
3. An aqueous solution of aniline hydrochloride ([latex]C_6H_5NH_3^+Cl^−[/latex]) is titrated with 0.050 M [latex]KOH[/latex].

Answer

a. The solution will be neutral at the equivalence point because sodium hydroxide is a strong base and hydrochloric acid is a strong acid.

b. The solution will be acidic at the equivalence point because ethylamine is a weak base and nitric acid is a strong acid.

c. The solution will be basic at the equivalence point because aniline hydrochloride is a weak acid and potassium hydroxide is a strong base.

Exercise 7.E.13

The pKa values of phenol red, bromophenol blue, and phenolphthalein are 7.4, 4.1, and 9.5, respectively. Which indicator is best suited for each acid–base titration?

1. titrating a solution of [latex]Ba(OH)_2[/latex] with 0.100 M [latex]HCl[/latex]
2. titrating a solution of trimethylamine ([latex]Me_3N[/latex]) with 0.150 M [latex]HNO_3[/latex]
3. titrating a solution of aniline hydrochloride ([latex]C_6H_5NH_3^+Cl^−[/latex]) with 0.050 M [latex]KOH[/latex]

Answer

a. Barium hydroxide is a strong base and hydrochloric acid is a strong acid thus phenol red with the [latex]pK_a=7.4[/latex] is best suited for the reaction.

b. Trimethylamine is a weak base and nitric acid is a strong acid thus bromophenol blue with the [latex]pK_a=4.1[/latex] is best suited for the reaction.

c. Aniline hydrochloride is a weak acid and potassium hydroxide is a strong base thus phenolphthalein with [latex]pK_a=9.5[/latex] is best suited for the reaction.

Exercise 7.E.14

a. For the titration of any strong acid with any strong base, the [latex]pH[/latex] at the equivalence point is 7.0. Why is this not usually the case in titrations of weak acids or weak bases?

b. Why are the titration curves for a strong acid with a strong base and a weak acid with a strong base identical in shape above the equivalence points but not below?

Answer

a. This is not usually the case in the titration of weak acids and weak bases because weak acids and weak bases would only ionize partially, thus complete neutralization does not occur.

b. The titration curve for a strong acid with a strong base is identical in shape above the equivalence point of the titration curve with a weak acid and strong base because both cases involve the addition of strong base. Not only does the strong base completely neutralize the acid but there is an excess of a strong base that makes the solution basic.

Exercise 7.E.15

Describe what is occurring on a molecular level during the titration of a weak acid, such as acetic acid, with a strong base, such as [latex]NaOH[/latex], at the following points along the titration curve. Which of these points corresponds to [latex]pH=pK_{a}[/latex]?

1. at the beginning of the titration
2. at the midpoint of the titration
3. at the equivalence point
4. when excess titrant has been added

Answer

a. The titration begins with a [latex]pH[/latex] is higher than the titration of a strong acid. At the beginning of the titration, there is a sharp increase in [latex]pH[/latex] because the anion of the weak acid becomes a common ion that reduces the ionization of the acid.

b. There is a sharp increase at the beginning of the titration that changes gradually due to the solution becoming a buffer. This continues until the strong base has overcome the buffer capacity. At the midpoint of the titration, the concentration of the weak acid is equal to the concentration of its conjugate base. This point is also known as half-neutralization because half the acid has been neutralized by the strong base.

c. At the equivalence point the pH is greater than 7 because the acid ([latex]HA[/latex]) has been converted to its conjugate base ([latex]A^{-}[/latex]) by sodium hydroxide and equilibrium moves backward toward the acid and produces hydroxide:

[latex]A^{-}+H_2O \rightleftharpoons AH+OH^{-}[/latex]

d. When the excess titrant has been added the solution becomes basic because sodium hydroxide completely neutralized the weak acid.

Exercise 7.E.16

On a molecular level, describe what is happening during the titration of a weak base, such as ammonia, with a strong acid, such as [latex]HCl[/latex], at the following points along the titration curve. Which of these points corresponds to [latex]pOH=pK_{b}[/latex]?

1. at the beginning of the titration
2. at the midpoint of the titration
3. at the equivalence point
4. when excess titrant has been added

Answer

a. The titration begins with a [latex]pH[/latex] that is lower than the titration of a strong base but higher than the [latex]pH=7[/latex]. At the beginning of the titration, there is a sharp decrease in [latex]pH[/latex] because the cation of the weak base becomes a common ion that reduces the ionization of the base.

b. The sharp decrease at the beginning of the titration changes gradually due to the solution becoming a buffer. This continues until the strong acid has overcome the buffer capacity. At the midpoint of the titration, the concentration of the weak base is equal to the concentration of its conjugate acid [latex]pH=pK_a[/latex]. This point is also known as half-neutralization because half the base has been neutralized by the strong acid.

c. At the equivalence point the [latex]pH[/latex] is less than 7 because the base [latex]NH_{3}[/latex] has been converted to its conjugate acid [latex]NH_{4}^{+}[/latex] by hydrochloric acid and equilibrium moves forwards toward the base and produces [latex]NH_{4}Cl^{-}[/latex]:

[latex]NH_{3}+HCl \rightleftharpoons NH_{4}Cl[/latex]

d. When excess titrant has been added the solution becomes acidic because hydrochloric acid completely neutralized the weak base.

Exercise 7.E.17

Calculate the pH at the following points in a titration of 40 mL (0.040 L) of 0.100 M barbituric acid (K_a = 9.8 × 10⁻⁵) with 0.100 M KOH.

(a) no KOH added

(b) 20 mL of KOH solution added

(c) 39 mL of KOH solution added

(d) 40 mL of KOH solution added

(e) 41 mL of KOH solution added

Answer

(a) pH = 2.50; (b) pH = 4.01; (c) pH = 5.60; (d) pH = 8.35; (e) pH = 11.08

Exercise 7.E.18

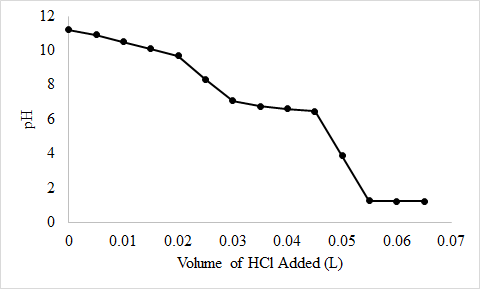
Calcium carbonate is a major contributor to the “hardness” of water. The amount of CaCO3 in a water sample can be determined by titrating the sample with an acid, such as HCl, which produces water and CO2. Write a balanced chemical equation for this reaction. Generate a plot of solution pH versus volume of 0.100 M HCl added for the titration of a solution of 250 mg of CaCO3 in 200.0 mL of water with 0.100 M HCl; assume that the HCl solution is added in 5.00 mL increments. What volume of HCl corresponds to the equivalence point?

Answer

[latex]CaCO_{3}\,(aq)+2\,HCl\,(aq) \rightarrow CaCl_{2}\,(aq)+H_2O\,(l)+CO_{2}\,(g)[/latex]
[latex]CO_{3}^{2-}\,(aq)+H^{+}\,(aq) \rightleftharpoons HCO_{3}^{-}\,(aq)[/latex]
[latex]HCO_{3}^{2-}\,(aq)+H^{+}\,(aq) \rightleftharpoons H_{2}CO_{3}\,(aq)[/latex]
[latex]K_{a1}=4.3 \times 10^{-7}[/latex]
[latex]K_{a2}=5.0 \times 10^{-11}[/latex]

At 0 mL addition of [latex]HCl[/latex]: [latex]pH=14-pOH=14-(-log(\sqrt{0.0125 \times \frac{10^{-14}}{5.0 \times 10^{-11}}})=11.20[/latex]

[latex]CaCO_{3}:250\,mg \times \frac{1\,g}{1,000\,mg} \times \frac{1\,mol}{100.0869\,g} \times \frac{1}{200\,mL \times \frac{1\,L}{1,000\,mL}}=0.0125\,M[/latex]

At 5 mL addition of [latex]HCl[/latex]: [latex]pH=-log(5 \times 10^{-11})+log(\frac{0.002}{0.0005})=10.9[/latex]

[latex]CaCO_{3}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.005\,L \times 0.1\,M=0.0005\,mol[/latex]

	[latex]CO_{3}^{2-}[/latex]	[latex]H^{+}[/latex]	[latex]HCO_{3}^{-}[/latex]
I	0.0025	0.0005	0
C	-0.0005	-0.0005	0.0005
E	0.002	0	0.0005

At 10 mL addition of [latex]HCl[/latex]: [latex]pH=-log(5 \times 10^{-11})+log(\frac{0.001}{0.0015})=10.5[/latex]

[latex]CaCO_{3}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.01\,L \times 0.1\,M=0.001\,mol[/latex]

	[latex]CO_{3}^{2-}[/latex]	[latex]H^{+}[/latex]	[latex]HCO_{3}^{-}[/latex]
I	0.0025	0.001	0
C	-0.001	-0.001	0.001
E	0.0015	0	0.001

At 15 mL addition of [latex]HCl[/latex]:[latex]pH=-log(5 \times 10^{-11})+log(\frac{0.001}{0.0015})=10.1[/latex]

[latex]CaCO_{3}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.015\,L \times 0.1\,M=0.0015\,mol[/latex]

	[latex]CO_{3}^{2-}[/latex]	[latex]H^{+}[/latex]	[latex]HCO_{3}^{-}[/latex]
I	0.0025	0.0015	0
C	-0.0015	-0.0015	0.0015
E	0.001	0	0.0015

At 20 mL addition of [latex]HCl[/latex]:[latex]pH=-log(5 \times 10^{-11})+log(\frac{5 \times 10^{-4}}{0.002})=9.7[/latex]

[latex]CaCO_{3}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.02\,L \times 0.1\,M=0.002\,mol[/latex]

	[latex]CO_{3}^{2-}[/latex]	[latex]H^{+}[/latex]	[latex]HCO_{3}^{-}[/latex]
I	0.0025	0.002	0
C	-0.002	-0.002	0.002
E	[latex]5 \times 10^{-4}[/latex]	0	0.002

At 25 mL addition of [latex]HCl[/latex]: first equivalence point: [latex]pH=\frac{-log(K_{a1})-log(K_{a2})}{2}=\frac{-log(4.3 \times 10^{-7})-log(5.0 \times 10^{-11})}{2}=8.33[/latex]

[latex]HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.025\,L \times 0.1\,M=0.0025\,mol[/latex]

	[latex]HCO_{3}^{-}[/latex]	[latex]H^{+}[/latex]	[latex]H_{2}CO_{3}[/latex]
I	0.0025	0.0025	0
C	-0.0025	-0.0025	0.0025
E	0	0	0.0025

At 30 mL addition of [latex]HCl[/latex]: [latex]pH=-log(4.3 \times 10^{-7})+log(\frac{0.0025}{0.0005})=7.07[/latex]

[latex]HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.03\,L \times 0.1\,M=0.003[/latex]

	[latex]HCO_{3}^{-}[/latex]	[latex]H^{+}[/latex]	[latex]H_{2}CO_{3}[/latex]
I	0.0025	0.003	0
C	-0.0025	-0.0025	0.0025
E	0	[latex]5 \times 10^{-4}[/latex]	0.0025

At 35 mL addition of [latex]HCl[/latex]: [latex]pH=-log(4.3 \times 10^{-7})+log(\frac{0.0025}{0.001})=6.76[/latex]

[latex]HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.035\,L \times 0.1\,M=0.0035[/latex]

	[latex]HCO_{3}^{-}[/latex]	[latex]H^{+}[/latex]	[latex]H_{2}CO_{3}[/latex]
I	0.0025	0.0035	0
C	-0.0025	-0.0025	0.0025
E	0	0.001	0.0025

At 40 mL addition of [latex]HCl[/latex]: [latex]pH=-log(4.3 \times 10^{-7})+log(\frac{0.0025}{0.003})=6.59[/latex]

[latex]HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.040\,L \times 0.1\,M=0.004[/latex]

	[latex]HCO_{3}^{-}[/latex]	[latex]H^{+}[/latex]	[latex]H_{2}CO_{3}[/latex]
I	0.0025	0.004	0
C	-0.0025	-0.0025	0.0025
E	0	0.0015	0.0025

At 45 mL addition of [latex]HCl[/latex]: [latex]pH=-log(4.3 \times 10^{-7})+log(\frac{0.0025}{0.002})=6.46[/latex]

[latex]HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.045\,L \times 0.1\,M=0.0045[/latex]

	[latex]HCO_{3}^{-}[/latex]	[latex]H^{+}[/latex]	[latex]H_{2}CO_{3}[/latex]
I	0.0025	0.0045	0
C	-0.0025	-0.0025	0.0025
E	0	0.002	0.0025

At 50 mL addition of [latex]HCl[/latex]: second equivalence point: [latex]pH=3.86[/latex]

[latex]HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.05\,L \times 0.1\,M=0.005[/latex]

	[latex]HCO_{3}^{-}[/latex]	[latex]H^{+}[/latex]	[latex]H_{2}CO_{3}[/latex]
I	0.0025	0.005	0
C	-0.0025	-0.0025	0.0025
E	0	0.0025	0.0025

At 55 mL addition of [latex]HCl[/latex]: [latex]pH=-log(\frac{0.003}{0.055})=1.26[/latex]

[latex]HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.055\,L \times 0.1\,M=0.0055[/latex]

	[latex]HCO_{3}^{-}[/latex]	[latex]H^{+}[/latex]	[latex]H_{2}CO_{3}[/latex]
I	0.0025	0.0055	0
C	-0.0025	-0.0025	0.0025
E	0	0.003	0.0025

At 60 mL addition of [latex]HCl[/latex]: [latex]pH=-log(\frac{0.0035}{0.06})=1.23[/latex]

[latex]HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.06\,L \times 0.1\,M=0.006[/latex]

	[latex]HCO_{3}^{-}[/latex]	[latex]H^{+}[/latex]	[latex]H_{2}CO_{3}[/latex]
I	0.0025	0.006	0
C	-0.0025	-0.0025	0.0025
E	0	0.0035	0.0025

At 65 mL addition of [latex]HCl[/latex]: [latex]pH=-log(\frac{0.0040}{0.065})=1.21[/latex]

[latex]HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol[/latex]
[latex]HCl: 0.06\,L \times 0.1\,M=0.006[/latex]

	[latex]HCO_{3}^{-}[/latex]	[latex]H^{+}[/latex]	[latex]H_{2}CO_{3}[/latex]
I	0.0025	0.0065	0
C	-0.0025	-0.0025	0.0025
E	0	0.0040	0.0025

Exercise 7.E.19

1. Write an expression for K_sp for each salt.

1. [latex]AgI[/latex]
2. [latex]CaF_{2}[/latex]
3. [latex]PbCl_2[/latex]
4. [latex]Ag_{2}CrO_{4}[/latex]

Answer

a. [latex]K_{sp}=[Ag^{+}][I^{-}][/latex]

b. [latex]K_{sp}=[Ca^{2+}][F^{-}]^{2}[/latex]

c. [latex]K_{sp}=[Pb^{2+}][Cl^{-}]^{2}[/latex]

d. [latex]K_{sp}=[Ag^{+}]^{2}[CrO_{4}^{2-}][/latex]

Exercise 7.E.20

Some species are not represented in a solubility product expression. Why?

Answer

The solubility constant expression, [latex]K_{sp}[/latex] is an equilibrium constant for a solid substance dissolving in a an aqueous solution. Thus, it is a measure of solubility and species that do not dissolve are not represented in the solubility product expression.

Exercise 7.E.21

How can an ion product be used to determine whether a solution is saturated?

Answer

An ion product can be used to determine whether a solution is saturated as it is compared to [latex]K_{sp}[/latex] where there are three possible conditions for an aqueous solution of an ionic solid:

[latex]Q

[latex]Q=K_{sp}[/latex]. The solution is saturated and at equilibrium.

[latex]Q>K_{sp}[/latex]. The solution is supersaturated, and ionic solid will precipitate.

Exercise 7.E.22

Predict the molar solubility of each compound using the K_sp values given.

1. Li₃PO₄: 2.37 × 10⁻¹¹
2. Ca(IO₃)₂: 6.47 × 10⁻⁶
3. Y(IO₃)₃: 1.12 × 10⁻¹⁰

Answer

a. [latex]K_{sp}=[Li^{+}]^{3}[PO_{4}^{3-}] \rightarrow 2.37 \times 10^{-11}=(3x)^{3}(x) \rightarrow x=9.68 \times 10^{-4}[/latex]

b. [latex]K_{sp}=[Ca^{2+}][IO_{3}^{-}]^{2} \rightarrow 6.47 \times 10^{-6}=(x)(2x)^{2} \rightarrow 1.17 \times 10^{-2}[/latex]

c. [latex]K_{sp}=[Y^{3+}][IO_{3}]^{-}]^{3} \rightarrow 1.12 \times 10^{-10}=(x)(3x)^{3} \rightarrow x=1.42 \times 10^{-3}[/latex]

3. [latex]0.750\,L \times \frac{0.0144\,mol}{1\,L} \times \frac{311.199\,g}{1\,mol}=3.37\,g[/latex]

[latex]K_{sp}=[Ag^{+}]^{2}[SO_{4}^{2-}] \rightarrow 1.20 \times 10^{-5}=(2x)^{2}(x) \rightarrow x=0.0144[/latex]

Exercise 7.E.23

A student prepared 750 mL of a saturated solution of silver sulfate (Ag₂SO₄). How many grams of Ag₂SO₄ does the solution contain? K_sp = 1.20 × 10⁻⁵.

Answer

[latex]0.750\,L \times \frac{0.0144\,mol}{1\,L} \times \frac{311.199\,g}{1\,mol}=3.37\,g[/latex]
[latex]K_{sp}=[Ag^{+}]^{2}[SO_{4}^{2-}] \rightarrow 1.20 \times 10^{-5}=(2x)^{2}(x) \rightarrow x=0.0144[/latex]

Exercise 7.E.24

Predict the molar concentration of each species in a saturated aqueous solution.

1. silver(I) bromide, AgBr, K_sp = 5.35 x 10^-13
2. lead(I) oxalate, PbC₂O₄, K_sp = 8.5 x 10^-9
3. iron(II) carbonate, FeCO₃, K_sp = 3.13 x 10^-11
4. silver(I) phosphate, Ag₃PO₄, K_sp = 8.89 x 10^-17
5. copper(I) cyanide, CuCN, K_sp = 3.47 x 10^-20

Answer

a. [latex]K_{sp}=[Ag^{+}][Br^{-}] \rightarrow 5.35 \times 10^{-13}=(x)(x) \rightarrow x=7.31 \times 10^{-7}[/latex]

b. [latex]K_{sp}=[PB^{2+}][C_{2}O_{4}] \rightarrow 8.5 \times 10^{-9}=(x)(x) \rightarrow x=9.2 \times 10^{-5}[/latex]

c. [latex]K_{sp}=[Fe^{2+}][CO_{3}^{2-}] \rightarrow 3.13 \times 10^{-11}=(x)(x) \rightarrow x=5.60 \times 10^{-6}[/latex]

d. [latex]K_{sp}=[Ag^{+}]^{3}[PO_{4}^{3-}] \rightarrow 8.89 \times 10^{-17}=(3x)^{3}(x) \rightarrow x=4.26 \times 10^{-5}[/latex]

e. [latex]K_{sp}=[Cu][CN] \rightarrow 3.47 \times 10^{-20}=(x)(x) \rightarrow x=1.86 \times 10^{-10}[/latex]

Exercise 7.E.25

From the solubility data given, calculate K_sp for each compound.

1. AgI: 2.89 × 10⁻⁷ g/100 mL
2. SrF₂: 1.22 × 10⁻² g/100 mL
3. Pb(OH)₂: 78 mg/500 mL
4. BiAsO₄: 14.4 mg/2.0 L

Answer

a. [latex]K_{sp}=[Ag^{+}][I^{-}]=x^{2}=(1.23 \times 10^{-8})^{2})=1.52 \times 10^{-16}[/latex]

[latex]AgI: (2.89 \times 10^{-7}\,g \times \frac{1\,mol}{234.77\,g} \times \frac{1}{0.1\,L}=1.23 \times 10^{-8}[/latex]

b. [latex]K_{sp}=[Sr^{2+}][F^{-}]^{2}]=(x)(2x)^{2}=4x^{3}=4(9.72 \times 10^{-4})^{3}=3.66 \times 10^{-9}[/latex]

[latex]SrF_{2}=1.22 \times 10^{-2}\,g \times \frac{1\,mol}{125.62\,g} \times \frac{1}{0.1\,L}=9.72 \times 10^{-4}[/latex]

c. [latex]K_{sp}=[Pb^{2+}][OH^{-}]^{2}=4x^{3}=4(6.47 \times 10^{-4})^{3}=1.08 \times 10^{-9}[/latex]

[latex]Pb(OH)_{2}=0.078\,g \times \frac{1\,mol}{241.21\,g} \times \frac{1}{0.1\,L}=6.47 \times 10^{-4}[/latex]

d. [latex]K_{sp}=[Bi^{3+}][AsO_{4}^{3-}]=x^{2}=(2.05 \times 10^{-5})^{2} =4.21 \times 10^{-10}[/latex]

[latex]BiAsO_{4}=0.0144\,g \times \frac{1\,mol}{350.924\,g} \times \frac{1}{2\,L}=2.05 \times 10^{-5}[/latex]

Exercise 7.E.26

You have calculated that 24.6 mg of BaSO₄ will dissolve in 1.0 L of water at 25°C. After adding your calculated amount to 1.0 L of water and stirring for several hours, you notice that the solution contains undissolved solid. After carefully filtering the solution and drying the solid, you find that 22.1 mg did not dissolve. According to your measurements, what is the K_sp of barium sulfate?

Answer

[latex]K_{sp}=[Ba^{2+}][SO_{4}^{2-}]=(x)(x)=x^{2}=(1.07 \times 10^{-5}\,M)^{2}=1.15 \times 10^{-10}[/latex]
[latex]BaSO_{4}:(24.6-22.1\,mg) \times \frac{1\,g}{1,000\,mg} \times \frac{1\,mol}{233.38\,g} \times \frac{1}{1.0\,L}=1.07 \times 10^{-5}\,M[/latex]

Exercise 7.E.27

Explain why the presence of MgCl₂ decreases the molar solubility of the sparingly soluble salt MgCO₃.

Answer

Because of the common ion effect. Adding a soluble Mg²⁺ salt increases [Mg2+] in solution, and Le Chatelier’s principle predicts that this will shift the solubility equilibrium of MgCO₃ to the left, decreasing its solubility.

Exercise 7.E.28

The K_sp of the phosphate fertilizer CaHPO₄·2H₂O is 2.7 × 10⁻⁷ at 25°C. What is the molar concentration of a saturated solution? What mass of this compound will dissolve in 3.0 L of water at this temperature?

Answer

[latex]K_{sp}=[Ca^{2+}][HPO_{4}^{2-}] \rightarrow 2.7 \times 10^{-7}=x^{2} \rightarrow x=5.2 \times 10^{-4}[/latex]
[latex]CaHPO4·2H2O: 3.0\,L \times \frac{2.7 \times 10^{-7}\,mol}{1\,L} \times \frac{290.1299\,g}{1\,mol}=2.35 \times 10^{-4}\,g[/latex]

Exercise 7.E.29

Use the data in Reference Table E3 to predict whether precipitation will occur when each pair of solutions is mixed.

1. 150 mL of 0.142 M Ba(NO₃)₂ with 200 mL of 0.089 M NaF
2. 250 mL of 0.079 M K₂CrO₄ with 175 mL of 0.087 M CaCl₂
3. 300 mL of 0.109 M MgCl₂ with 230 mL of 0.073 M Na₂(C₂O₄)

Answer

a. [latex]Q=[Ba^{2+}][F^{-}]^{2}=(0.060857)(0.05643)^{2}=1.94 \times 10^{-4}>1.84 \times 10^{-7}[/latex] Therefore, precipitate will form.

[latex]Ba^{2+}: \frac{(0.150)(0.142)}{0.35}=0.060857[/latex]
[latex]F^{-}: \frac{(0.25)(0.079)}{0.35}=0.05643[/latex]

b. [latex]Q=[K^{+}][Cl^{-}]=(0.0465)(0.0358)=1.66 \times 10^{-3}<21.7. Therefore, precipitate will not form.

[latex]K^{+}: \frac{(0.25)(0.079)}{0.425}=0.0465[/latex]
[latex]Cl^{-}: \frac{(0.175)(0.087)}{0.425}=0.0358[/latex]

c. [latex]Q=[Mg^{2+}][C_{2}O_{4}^{2-}]=(0.0617)(0.0317)=1.95 \times 10^{-3}>8.5 \times 10^{-5}[/latex] Therefore, precipitate will form.

[latex]Mg^{2+}:\frac{(0.3)(0.109)}{0.53}=0.0617[/latex]
[latex]C_{2}O_{4}: \frac{(0.23)(0.073)}{0.53}=0.0317[/latex]