7.2: Practical Aspects of Buffers
Skills to Develop
- Understand the factors that affect buffer range and capacity
- Calculate the amounts of acid and base needed to prepare a buffer of a given pH
Buffers are characterized by the pH range over which they can maintain a more or less constant pH and by their buffer capacity, the amount of strong acid or base that can be absorbed before the pH changes significantly. Although the useful pH range of a buffer depends strongly on the chemical properties of the weak acid and weak base used to prepare the buffer (i.e., on [latex]K[/latex]), its buffer capacity depends solely on the concentrations of the species in the buffered solution.
Buffer Capacity
Buffer solutions do not have an unlimited capacity to keep the pH relatively constant (Figure 7.2.1). If we add so much base to a buffer that the weak acid is exhausted, no more buffering action toward the base is possible. On the other hand, if we add an excess of acid, the weak base would be exhausted, and no more buffering action toward any additional acid would be possible. In fact, we do not even need to exhaust all of the acid or base in a buffer to overwhelm it; its buffering action will diminish rapidly as a given component nears depletion.

The buffer capacity is the amount of acid or base that can be added to a given volume of a buffer solution before the pH changes significantly, usually by one unit. Buffer capacity depends on the amounts of the weak acid and its conjugate base that are in a buffer mixture.
The more concentrated the buffer solution, the greater its buffer capacity.
As illustrated in Figure 7.2.2, when [latex]NaOH[/latex] is added to solutions that contain different concentrations of an acetic acid/sodium acetate buffer, the observed change in the pH of the buffer is inversely proportional to the concentration of the buffer. If the buffer capacity is 10 times larger, then the buffer solution can absorb 10 times more strong acid or base before undergoing a significant change in pH.
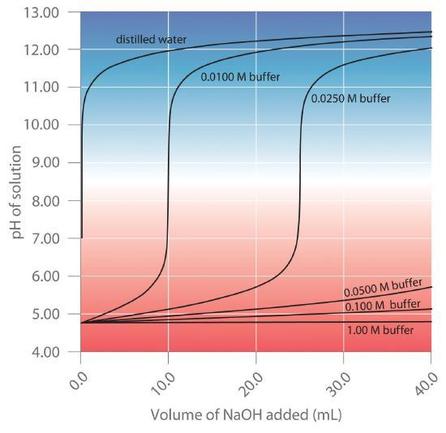
A buffer maintains a relatively constant pH when acid or base is added to a solution. The addition of even tiny volumes of 0.10 M [latex]NaOH[/latex] to 100.0 mL of distilled water results in a very large change in pH. As the concentration of a 50:50 mixture of sodium acetate/acetic acid buffer in the solution is increased from 0.010 M to 1.00 M, the change in the pH produced by the addition of the same volume of [latex]NaOH[/latex] solution decreases steadily. For buffer concentrations of at least 0.500 M, the addition of even 25 mL of the [latex]NaOH[/latex] solution results in only a relatively small change in pH.
Buffer Range
The buffer range is the range of pH values over which a buffer is most effective (i.e. has the largest buffer capacity for its concentration). A good buffer mixture should have about equal concentrations of both of its components. As a rule of thumb, a buffer solution has generally lost its usefulness when one component of the buffer pair is less than about 10% of the other. Figure 7.2.3 shows an acetic acid-acetate ion buffer as base is added. The initial pH is 4.74 (the [latex]pK_a[/latex] of acetic acid). A change of 1 pH unit occurs when the acetic acid concentration is reduced to 11% of the acetate ion concentration. Past this point, the pH begins to change more rapidly with additional base as the buffer is overwhelmed.
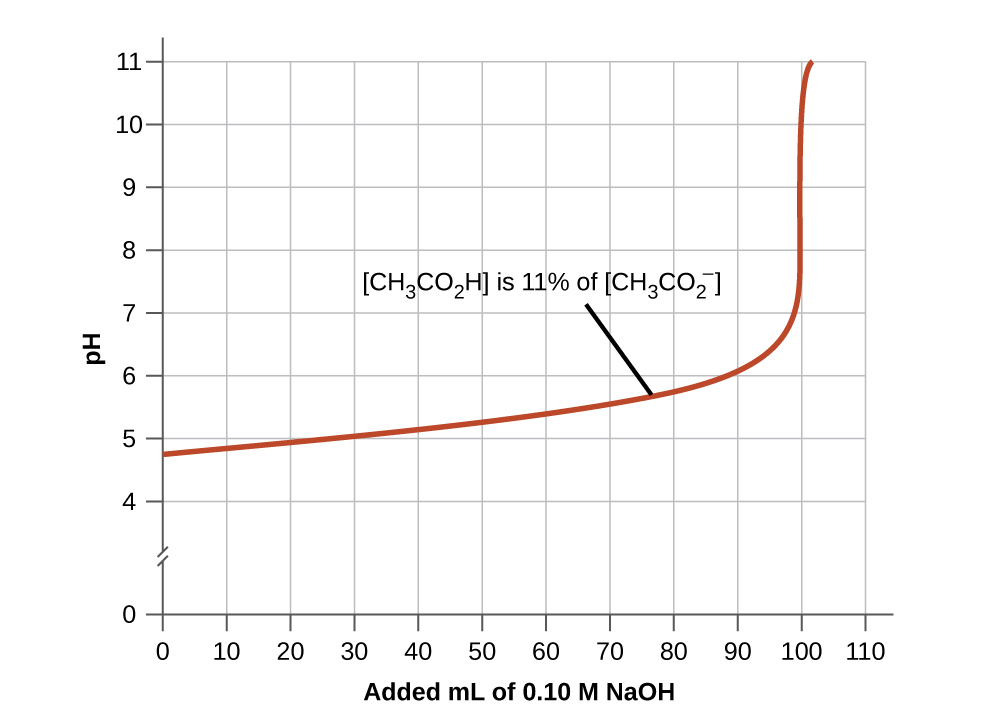
Figure 7.2.3: The graph, an illustration of buffering action, shows change of pH as an increasing amount of a 0.10-M NaOH solution is added to 100 mL of a buffer solution in which, initially, [CH3CO2H] = 0.10 M and [latex]\ce{[CH3CO2- ]}=0.10\:M[/latex]
The most effective buffers contain equal concentrations of an acid and its conjugate base.
A buffer that contains approximately equal amounts of a weak acid and its conjugate base in solution is equally effective at neutralizing either added base or added acid. This is shown in Figure 7.2.4 for an acetic acid/sodium acetate buffer. Adding a given amount of strong acid shifts the system along the horizontal axis to the left, whereas adding the same amount of strong base shifts the system the same distance to the right. In either case, the change in the ratio of [latex]CH_3CO_2^−[/latex] to [latex]CH_3CO_2H[/latex] from 1:1 reduces the buffer capacity of the solution.
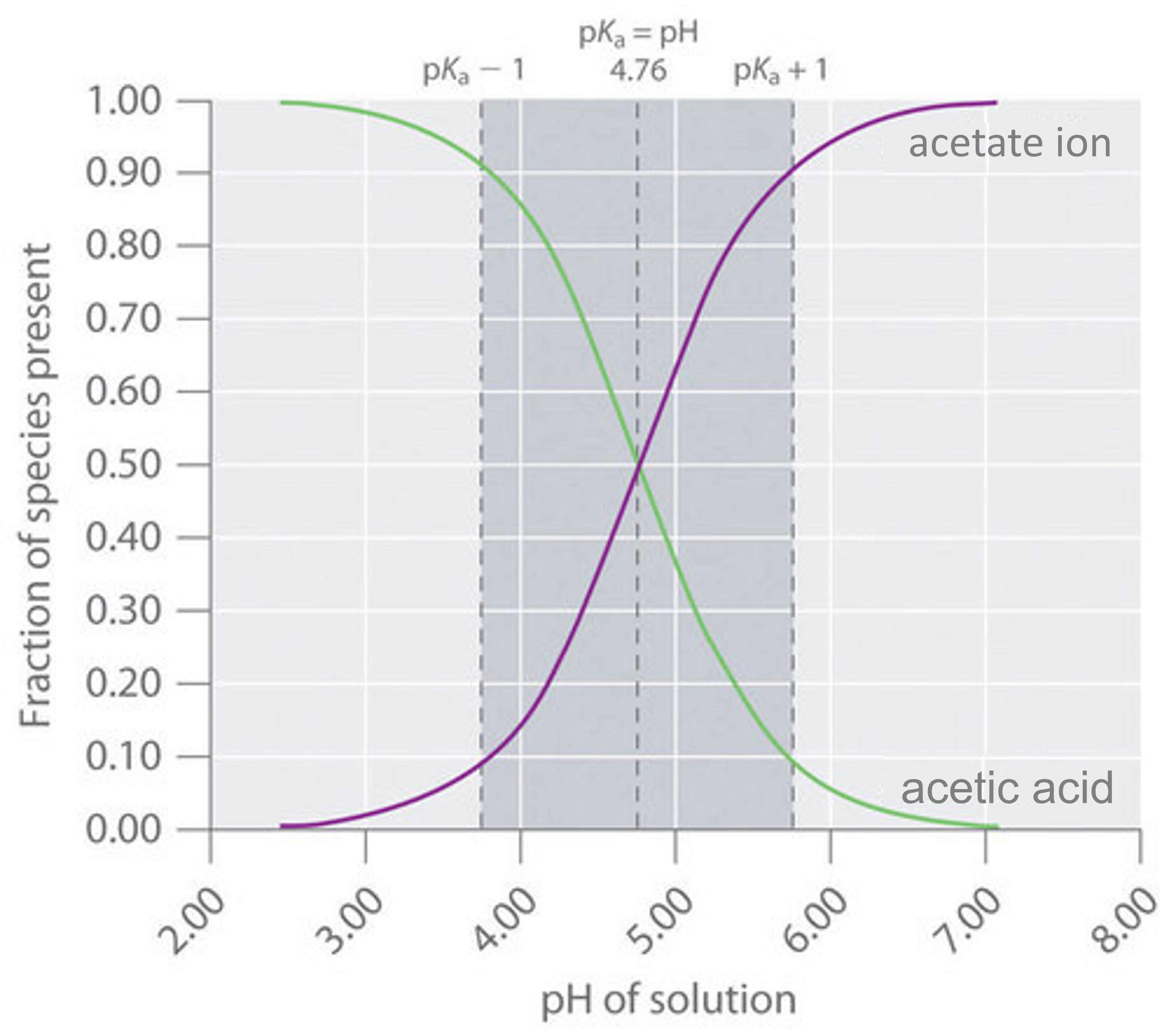
Recall that according to the Henderson-Hasselbalch relationship, pH = [latex]pK_a[/latex] when a buffer contains equal concentrations of conjugate acid and base. Thus, the effective range of a buffer is approximately the [latex]pK_a[/latex] plus or minus one pH unit. This corresponds to a ten-to-one concentration of the two components either way, as illustrated above.
The buffer range is approximately [latex]pH = pK_a \pm 1[/latex]
Preparing Buffers
In many situations, chemists must prepare buffer solutions to maintain a desired pH. There are many different buffer systems to choose from, depending on the characteristics and pH required of the solution. The following steps may be used when preparing a buffer in the laboratory:
- Choose an appropriate buffer system. Because the buffer capacity is highest where pH = [latex]pK_a[/latex], the ideal buffer will have a [latex]pK_a[/latex] close to the desired pH. In general, weak acids and their salts are better as buffers for pHs less than 7; weak bases and their salts are better as buffers for pHs greater than 7.
- Use the total buffer concentration and pH desired to calculate the amounts of acid and base needed to create the buffer. The Henderson-Hasselbalch equation can be used to determine the ratio of [base]/[acid] needed.
- Mix the components. The weak acid can be added to a salt of the conjugate base directly; alternatively, enough strong base can be added to the weak acid to partially convert it to the conjugate base (or strong acid can be added to a weak base to partially neutralize it).
- Adjust the pH as desired. In practice, experimental error and other factors often cause buffers not quite to be at the calculated pH, so the chemist can add small amounts of strong acid or strong base to fine-tune the pH, monitoring the solution with a pH meter.
Example 7.2.1 illustrates the method for calculating the amount of reagents needed to create a buffer at a desired pH.
Example 7.2.1
The [latex]pK_a[/latex] of formic acid is 3.75. How many grams of formic acid ([latex]HCO_2H[/latex]) and sodium formate ([latex]HCO_2Na[/latex]) must be mixed to prepare 100.0 mL of a buffer with a total concentration of 0.100 M and a pH of 3.90?
Given: [latex]pK_a[/latex] of formic acid, volume of buffer, total buffer concentration, desired pH
Asked For: grams of [latex]HCO_2H[/latex] and [latex]HCO_2Na[/latex]
Strategy: Use the Henderson-Hasselbalch approximation to determine the ratio of [base]/[acid] needed, then use the total concentration and volume to calculate the number of moles of each component needed, convert moles to grams
Solution:
According to the Henderson-Hasselbalch approximation,
[latex]pH = pK_a + \log([base]/[acid])[/latex]
In this case, the conjugate base is [latex]HCO_2Na[/latex] and the conjugate acid is [latex]HCO_2H[/latex]. Plugging the desired pH and [latex]pK_a[/latex] into the equation:
[latex]3.90 = 3.75 + \log([HCO_2Na]/[HCO_2H])[/latex]
Solving for the [base]/[acid] ratio:
[latex]\log([HCO_2Na]/[HCO_2H]) = 0.15[/latex]
[latex][HCO_2Na]/[HCO_2H] = e^{0.15} = 1.16[/latex]
This ratio means that the buffer must contain 1.16 times as many moles of [latex]HCO_2Na[/latex] as [latex]HCO_2H[/latex] to get a pH of 3.90. This makes sense because the desired pH is higher than the [latex]pK_a[/latex], so more of the conjugate base than acid is needed.
We know that we need to create 100.0 mL of buffer with a total concentration of 0.100 M:
[latex]\mathrm{100.0 mL×\dfrac{1 L}{1000 mL}×\dfrac{0.100 mol}{1 L}= 0.0100\:mol}[/latex]
Thus, we need 0.0100 moles total of both buffer components. We can set up the following two equations:
[latex]\mathrm{mol(HCO_2Na) + mol(HCO_2H) = 0.0100\:mol}[/latex]
[latex]\mathrm{mol(HCO_2Na)/mol(HCO_2H) = 1.16}[/latex] or [latex]\mathrm{mol(HCO_2Na) = 1.16×mol(HCO_2H)}[/latex]
With two equations and two unknowns, we substitute one expression into the other to solve for both components:
[latex]\mathrm{1.16×mol(HCO_2H) + mol(HCO_2H) = 2.16×mol(HCO_2H) = 0.0100\:mol}[/latex]
[latex]\mathrm{mol(HCO_2H) = 0.00463\:mol\:HCO_2H}[/latex]
[latex]\mathrm{mol(HCO_2Na) = 1.16×0.00463\:mol = 0.00537\:mol\:HCO_2Na}[/latex]
Finally, we solve for grams using the molar mass of each component:
[latex]\mathrm{0.00463\:mol\:HCO_2H×\dfrac{46.03\:g}{1\:mol\:HCO_2H}=0.213\:g\:HCO_2H}[/latex]
[latex]\mathrm{0.00537\:mol\:HCO_2Na×\dfrac{68.01\:g}{1\:mol\:HCO_2Na}=0.365\:g\:HCO_2Na}[/latex]
Exercise 7.2.1
A biochemist requires 250 mL of a 0.15 M acetic acid-acetate buffer at pH 5.00. How many grams of [latex]CH_3CO_2H[/latex] and [latex]CH_3CO_2Na[/latex] must she add to create the buffer mixture (the [latex]pK_a[/latex] of acetic acid is 4.74)?
- Answer
-
0.98 g [latex]CH_3CO_2H[/latex] and 1.74 g [latex]CH_3CO_2Na[/latex]
Summary
Buffers are characterized by their pH range and buffer capacity. The useful pH range of a buffer depends on the chemical properties of the conjugate weak acid–base pair used to prepare the buffer and is generally the [latex]pK_a \pm 1[/latex]. Buffer capacity depends on the concentrations of the species in the solution; the more concentrated the buffer mixture, the higher the buffer capacity. A buffer has its highest capacity at equal concentrations of weak acid and conjugate base, when [latex]pH = pK_a[/latex].
